NumPy基础

约 7302 个字 930 行代码预计阅读时间 40 分钟

本章笔记将会涉及NumPy的基础用法，包含理解NumPy最重要的类ndarray.

在正式开始之前，请务必保证自己的环境里拥有NumPy。

# !/bin/bash
pip install numpy

本笔记使用的Python版本为3.12.3，是笔者常用的一个版本，实例程序无特殊说明均通过IPython交互进行。

本笔记的参考书是《Python for Data Analysis》，很好的书，使我的蟒蛇旋转。

从数组开始

什么是NumPy数组？

NumPy的源头在哪里？其的N维数组 (N-dimensional array, ndarray) 一定是最基础的那个，它是的你可以以向量的形式操作一整组数据（而且非常高效）。

接下来让我们来创建一个NumPy数组：

In [1]: import numpy as np

In [2]: data = np.array([[1.5, 0, 2], [-0.5, -1, 3]])

In [3]: data
Out[3]:
array([[ 1.5,  0. ,  2. ],
       [-0.5, -1. ,  3. ]])

然后，然后我们对其进行简单的运算：

In [4]: data * 10
Out[4]:
array([[ 15.,   0.,  20.],
       [ -5., -10.,  30.]])

In [5]: data + data
Out[5]:
array([[ 3.,  0.,  4.],
       [-1., -2.,  6.]])

Note

直接将NumPy全部导入项目中是不明智的，因为NumPy的命名空间极易与Python标准库冲突，现在的最佳实践如下：

import numpy as np

每一个ndarray都是用于同质数据的通用多维容器，即所有元素类型统一。每个数组都有两个属性，描述数组大小的shape与描述数组数据类型的dtype。

In [6]: data.shape
Out[6]: (2, 3)

In [7]: data.dtype
Out[7]: dtype('float64')

Tip

本笔记中，N维数组、数组、NumPy数组与"ndarray"是同义的。

创建数组

进入NumPy世界的第一步，就是学会创建一个数组，而NumPy支持任何序列类对象，比如数组本身，以及列表等。

什么样的对象是可以被转换的？

NumPy可以将序列类对象转换为数组，那什么样的对象被称为序列类呢？

实际上这涉及到了NumPy如何将一个非ndarray对象转化为数组的。

NumPy会检查其是否实现了__array__协议，也就是提供了__array__方法，并期待其返回一个numpy.ndarray对象。而__array_interface__是一个更底层的方法，它会直接暴露数据在内存中的布局，包括数据指针，形状与步长等等。典型的例子是pandas.Series。
如果不支持，NumPy会检查其是否支持序列协议，也就是提供了__len__与__getitem__方法，NumPy会通过前者确定分配多大的连续内存，通过后者一个个取出元素存入分配的内存中。
如果以上两个协议都不支持，NumPy会检查对象是否实现了迭代协议，也就是__iter__与__next__，即对象为一个迭代器对象。这种方法因为要动态调整分配内存从而开销较大。

接下来我们来试着创建几个数组：

In [1]: import numpy as np

In [2]: data = [1, 1.5, 2, 3]

In [3]: arr1 = np.array(data)

In [4]: arr1
Out[4]: array([1. , 1.5, 2. , 3. ])

In [5]: data2 = [[0, 1, 2.5, 4], [-1, -3, 4, 2.5]]

In [6]: arr2 = np.array(data2)

In [7]: arr2
Out[7]:
array([[ 0. ,  1. ,  2.5,  4. ],
       [-1. , -3. ,  4. ,  2.5]])

可以看到data2是一个嵌套数组，其也可以被正常转化为一个numpy.ndarray对象，而且是一个二维数组。通过属性numpy.ndarray.ndim可以查看数组维度:

In [8]: arr2.ndim
Out[8]: 2

In [9]: arr2.shape
Out[9]: (2, 4)

除非特别指定，否则numpy.array方法会尝试为创建数组推断一个数据类型，正如我们前文所见的float64，就是一个64位浮点数，当然还有更多类型，比如：

In [10]: data3 = [1, 2, 3]

In [11]: arr3 = np.array(data3)

In [12]: arr3.dtype
Out[12]: dtype('int64')

除了手动指定数组的数据内容，还可以通过其他方法创建一个特定的新数组：

In [13]: np.zeros(10)
Out[13]: array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])

In [14]: np.zeros((3, 6))
Out[14]:
array([[0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0.]])

In [15]: np.ones(5)
Out[15]: array([1., 1., 1., 1., 1.])

In [16]: np.empty(5)
Out[16]: array([1., 1., 1., 1., 1.])

其中numpy.zeros创建了一个全0的数组，而numpy.ones则是创建了一个全1的数组。numpy.empty比较特殊，它会创建一个全空的数组，不会给其中的任何元素赋初值，所以它实际上的输出取决于它当下被分配到的“脏内存”内容。

在上面的例子中，它刚好继承了numpy.ones(5)初始化过的空间，但这不意味着你可以相信其的数据内容，因为实际上它是未被初始化的。

如果想要创建一个更高维的数组，需要向其传入一个元组给shape参数来描述数组形状，正如上面所做的那样。

numpy.arange可以看成是Python range的数组版本：

In [17]: np.arange(15)
Out[17]: array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14])

Function	Description
array	将输入数据（列表、元组、数组或其他序列类型）转换为 ndarray，可通过推断数据类型或显式指定数据类型；默认情况下会复制输入数据
asarray	将输入转换为 ndarray，但如果输入已经是 ndarray，则不进行复制
arange	类似于内置的 range 函数，但返回的是 ndarray 而不是列表
ones, ones_like	生成指定形状和数据类型的全 1 数组；ones_like 接受另一个数组并生成与其形状和数据类型相同的全 1 数组
zeros, zeros_like	类似于 ones 和 ones_like，但生成的是全 0 数组
empty, empty_like	通过分配新内存创建新数组，但不会像 ones 和 zeros 那样填充任何值
full, full_like	生成指定形状和数据类型的数组，所有元素设置为指定的“填充值”；full_like 接受另一个数组并生成相同形状和数据类型的填充数组
eye, identity	创建一个 N × N 的单位矩阵（对角线为 1，其余位置为 0）

数组的数据类型

numpy.ndarray.dtype是一个包含了对应数组在内存中数据的类型的特殊对象，它决定了程序如何解释这段内存记录的数据，是以浮点数的形式，还是整数的形式？

在创建数组对象的时候，我们就可以手动指定dtype参数的值：

In [1]: import numpy as np

In [2]: arr1 = np.array([1, 2, 3], dtype=np.float64)

In [3]: arr2 = np.array([1, 2, 3], dtype=np.int32)

In [4]: arr1.dtype
Out[4]: dtype('float64')

In [5]: arr2.dtype
Out[5]: dtype('int32')

明确的数据类型意味着NumPy可以跨系统进行数据交互，也可以很方便的与C或Fortran编写的底层库进行无缝对接。数值型数据类型采用统一的命名规则：先指定数据类型名称 (float or int)，后表明其占用位数（如Python中双精度浮点数占据8个字节，也就是64位）。完整的数据类型可见下表。

Type	Type code	Description
int8, uint8	i1, u1	有符号和无符号 8 位（1 字节）整数类型
int16, uint16	i2, u2	有符号和无符号 16 位整数类型
int32, uint32	i4, u4	有符号和无符号 32 位整数类型
int64, uint64	i8, u8	有符号和无符号 64 位整数类型
float16	f2	半精度浮点数
float32	f4 或 f	标准单精度浮点数；与 C 语言中的 float 兼容
float64	f8 或 d	标准双精度浮点数；与 C 语言中的 double 和 Python 的 float 对象兼容
float128	f16 或 g	扩展精度浮点数
complex64, complex128, complex256	c8, c16, c32	复数，分别由两个 32、64 或 128 位浮点数表示
bool	?	布尔类型，存储 True 和 False 值
object	O	Python 对象类型；值可以是任意 Python 对象
string_	S	固定长度 ASCII 字符串类型（每个字符 1 字节）；例如，要创建长度为 10 的字符串数据类型，使用 'S10'
unicode_	U	固定长度 Unicode 类型（字节数平台相关）；语义与 string_ 相同（例如，'U10'）

ndarray提供了astype方法来显式地转化数据类型：

In [6]: arr = np.array([1, 2, 3, 4])

In [7]: arr.dtype
Out[7]: dtype('int64')

In [8]: float_arr = arr.astype(np.float64)

In [9]: float_arr.dtype
Out[9]: dtype('float64')

In [10]: arr = np.array([1.5, 2.3, 3.1, 4.5])

In [11]: arr
Out[11]: array([1.5, 2.3, 3.1, 4.5])

In [12]: arr.astype(np.int32)
Out[12]: array([1, 2, 3, 4], dtype=int32)

如果有一串以字符形式表达的数字，同样可以被正确的转化为对应的数据类型，正如Python中的int与float那样。

In [13]: numeric_strings = np.array(["1.25", "-9.6", "42"], dtype=np.bytes_)

In [14]: numeric_strings.astype(float)
Out[14]: array([ 1.25, -9.6 , 42.  ])

正如上面演示的那样，我们可以用Python内置的数据类型来指定dtype属性，NumPy会自动进行转化。同样你可以使用之前表格给出的数据类型简写来指定。

Note

astype方法总会返回一个新数组，而不会原位修改。

数组的数学运算

数组的强大之处在于你可以批量的操作一组数据，而无需通过for循环，这在较大数据对象下被认为是极其低效的，这种特性被称为向量化。数组的数学运算分为两类：形状相同的数组间的数学运算与数组和标量间的数学运算。

形状相同的数组间的数学运算会以元素为单位进行运算：

In [1]: import numpy as np

In [2]: arr = np.array([[1, 2, 3], [4, 5, 6]])

In [3]: arr
Out[3]:
array([[1, 2, 3],
       [4, 5, 6]])

In [4]: arr * arr
Out[4]:
array([[ 1,  4,  9],
       [16, 25, 36]])

In [5]: arr - arr
Out[5]:
array([[0, 0, 0],
       [0, 0, 0]])

形状相同的数组间进行布尔运算同样以元素为单位进行，但是返回的数组以布尔值填充：

In [6]: arr1 = np.array([[1, 4, 3], [2, 5, 7]])

In [7]: arr1 == arr
Out[7]:
array([[ True, False,  True],
       [False,  True, False]])

数组与标量之间的数学运算，会将标量应用在数组的每个元素上：

In [8]: 1 / arr
Out[8]:
array([[1.        , 0.5       , 0.33333333],
       [0.25      , 0.2       , 0.16666667]])

In [9]: arr ** 2
Out[9]:
array([[ 1,  4,  9],
       [16, 25, 36]])

数组与标量之间的布尔运算，同样会将标量应用在数组的每个元素上，但是返回数组以布尔值填充：

In [10]: arr == 2
Out[10]:
array([[False,  True, False],
       [False, False, False]])

Note

不同形状数组之间的运算被称之为广播 (broadcasting)，这属于进阶内容。

数组的索引与切片

NumPy中数组提供了丰富的索引与切片方式帮助你方便的选择特定的子集或单独的元素，对于一维数组来说，它的行为与Python中的列表类似：

In [1]: import numpy as np

In [2]: arr = np.arange(10)

In [3]: arr
Out[3]: array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

In [4]: arr[5]
Out[4]: np.int64(5)

In [5]: arr[5:8]
Out[5]: array([5, 6, 7])

In [6]: arr[5:8] = 12

In [7]: arr
Out[7]: array([ 0,  1,  2,  3,  4, 12, 12, 12,  8,  9])

如你所见，arr[5:8] = 12批量修改了三个索引上的元素的值，这种特性被称为广播。

视图对象

与Python内置列表相比，第一个重要区别就是数组切片是对原始数据的一个视图，所有对视图的修改都会反应到原始数组上。

In [8]: arr1 = np.array([[1, 2, 3], [4, 5, 6]])

In [9]: arr2 = arr1[:,1:]

In [10]: arr1
Out[10]:
array([[1, 2, 3],
    [4, 5, 6]])

In [11]: arr2
Out[11]:
array([[2, 3],
    [5, 6]])

In [12]: arr2[1, 0] = 7

In [13]: arr2
Out[13]:
array([[2, 3],
    [7, 6]])

In [14]: arr1
Out[14]:
array([[1, 2, 3],
    [4, 7, 6]])

这种设计的初衷是考虑到NumPy在处理大量数据的时候避免频繁的数据复制，这会带来严重的性能问题。如果你确实想复制数据而不是原位修改它，使用copy()方法是一个不错的选择。

In [15]: arr3 = arr1.copy()

In [16]: arr3
Out[16]:
array([[1, 2, 3],
    [4, 7, 6]])

In [17]: arr1
Out[17]:
array([[1, 2, 3],
    [4, 7, 6]])

In [18]: arr3[1, 0] = 5

In [19]: arr3
Out[19]:
array([[1, 2, 3],
    [5, 7, 6]])

In [20]: arr1
Out[20]:
array([[1, 2, 3],
    [4, 7, 6]])

使用裸切片[:]会分配原数组中所有的值：

In [21]: arr4 = arr1[:]

In [22]: arr1
Out[22]:
array([[1, 2, 3],
       [4, 7, 6]])

In [23]: arr4
Out[23]:
array([[1, 2, 3],
       [4, 7, 6]])

如果你创建了一个二维数组，则索引就会复杂很多，相比一维数组，对二维数组进行单索引引用只会返回一个一维数组，但是你可以继续递归的索引元素，或者使用逗号分隔的索引列表来访问对应的元素：

In [24]: arr2d = np.array([[1, 2, 3], [4, 5, 6]])

In [25]: arr2d[0]
Out[25]: array([1, 2, 3])

In [26]: arr2d[0][2]
Out[26]: np.int64(3)

In [27]: arr2d[0, 2]
Out[27]: np.int64(3)

实际上，你可以将二维数组想象为一张平面表格，纵向上为行的变化，横向上为列的变化，其中第一个索引代表行号，第二个索引代表列号。

在更高维的数组中同样如此，值得注意的是，如果忽略了更低维度的索引，返回的对象将是一个低维数组，可以将它视为在你最后一个索引所对应的维度上的一个元素。

数组的索引可以用来选择指定位置的元素，同时可以通过广播的方式操作索引的元素或者是数组之间的赋值。

现在让我们来进一步探索一下切片这件事。实际上切片可以看成一种范围索引，自然的我们可以独立在各个维度上选取切片范围：

In [28]: arr2d = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

In [29]: arr2d
Out[29]:
array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])

In [30]: arr2d[:2, 1:]
Out[30]:
array([[2, 3],
       [5, 6]])

当然，通过数值索引与切片索引，我们可以获得更低维度的数组切片（但这不影响其还是原数组的一个视图）：

In [31]: lower_dim_slice = arr2d[1, :2]

In [32]: lower_dim_slice.shape
Out[32]: (2,)

值得注意的是，裸冒号代表坐标轴本身：

In [33]: arr2d[:,:1]
Out[33]:
array([[1],
       [4],
       [7]])

对切片表达式进行赋值，会广播于切片范围内的所有元素：

In [34]: arr2d[:2, 1:] = 0

In [35]: arr2d
Out[35]:
array([[1, 0, 0],
       [4, 0, 0],
       [7, 8, 9]])

布尔索引

NumPy库支持使用布尔值来做索引，现在假设我们有一个带有数据的数组和一个带有重复名字的数组：

In [1]: import numpy as np

In [2]: names = np.array(["Bob", "Joe", "Will", "Bob", "Will", "Joe", "Joe"])

In [3]: data = np.array([[4, 7], [0, 2], [-5, 6], [0, 0], [1, 2], [-12, -4], [3, 4]])

In [4]: names
Out[4]: array(['Bob', 'Joe', 'Will', 'Bob', 'Will', 'Joe', 'Joe'], dtype='<U4')

In [5]: data
Out[5]:
array([[  4,   7],
       [  0,   2],
       [ -5,   6],
       [  0,   0],
       [  1,   2],
       [-12,  -4],
       [  3,   4]])

然后通过比较，我们可以从名字数组中获得一个布尔数组：

In [6]: names == 'Bob'
Out[6]: array([ True, False, False,  True, False, False, False])

我们可以将这个布尔数组传递给数据数组作为索引：

In [7]: data[names == 'Bob']
Out[7]:
array([[4, 7],
       [0, 0]])

我们可以认为布尔数组本身就是对一个轴上的索引，所以面对多维数组的时候，可以混合使用布尔索引、数值索引和切片索引：

In [8]: data[names == 'Bob', 1:]
Out[8]:
array([[7],
       [0]])

In [9]: data[names == 'Bob', 1]
Out[9]: array([7, 0])

想要选择除了"Bob"以外的所有名字？NumPy支持!=或~两种方式！

In [10]: names != 'Bob'
Out[10]: array([False,  True,  True, False,  True,  True,  True])

In [11]: ~(names == 'Bob')
Out[11]: array([False,  True,  True, False,  True,  True,  True])

In [12]: data[names != 'Bob']
Out[12]:
array([[  0,   2],
       [ -5,   6],
       [  1,   2],
       [-12,  -4],
       [  3,   4]])

实际上~是一个很方便的运算符，当你想要反转一个布尔数组时候：

In [13]: cond = names == 'Bob'

In [14]: data[~cond]
Out[14]:
array([[  0,   2],
       [ -5,   6],
       [  1,   2],
       [-12,  -4],
       [  3,   4]])

数组支持&（与运算）和 |（或运算）：

In [15]: mask = (names == 'Bob') | (names == 'Will')

In [16]: mask
Out[16]: array([ True, False,  True,  True,  True, False, False])

In [17]: data[mask]
Out[17]:
array([[ 4,  7],
       [-5,  6],
       [ 0,  0],
       [ 1,  2]])

Tip

Python原生支持and和or关键字，但NumPy的数组并不支持，它的同义关键字是&与|。

使用布尔索引可以很方便对特定条件的数据进行操作：

In [18]: data[data<0] = 0

In [19]: data
Out[19]:
array([[4, 7],
       [0, 2],
       [0, 6],
       [0, 0],
       [1, 2],
       [0, 0],
       [3, 4]])

Note

使用布尔索引索引原数组并将值赋值给新变量的过程中会直接创建一个数据的副本，而不是数值索引或切片索引会返回一个原数据的视图。

花式索引

花式索引是NumPy官方对整数数组或整数列表索引的别称，前面我们就已了解过如何对一个ndarray做整数索引：

In [1]: import numpy as np

In [2]: arr = np.zeros((8,4))

In [3]: for i in range(8):
   ...:     arr[i] = i
   ...:

In [4]: arr
Out[4]:
array([[0., 0., 0., 0.],
       [1., 1., 1., 1.],
       [2., 2., 2., 2.],
       [3., 3., 3., 3.],
       [4., 4., 4., 4.],
       [5., 5., 5., 5.],
       [6., 6., 6., 6.],
       [7., 7., 7., 7.]])

使用花式索引则可以传入一个整数数组或整数列表来一次性选取多行，使用负数索引可以反向索引：

In [5]: arr[[4, 3, 0, 6]]
Out[5]:
array([[4., 4., 4., 4.],
       [3., 3., 3., 3.],
       [0., 0., 0., 0.],
       [6., 6., 6., 6.]])

In [6]: arr[[-3, -5, -7]]
Out[6]:
array([[5., 5., 5., 5.],
       [3., 3., 3., 3.],
       [1., 1., 1., 1.]])

传入多个整数数组或整数列表可以索引得到一个一维数组，其中每一个元素取决于所有整数数组或整数列表对应位置上整数索引所构成的对单一元素的索引：

In [8]: arr
Out[8]:
array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11],
       [12, 13, 14, 15],
       [16, 17, 18, 19],
       [20, 21, 22, 23],
       [24, 25, 26, 27],
       [28, 29, 30, 31]])

In [9]: arr[[1, 3, 5, 7], [0, 1, 2, 3]]
Out[9]: array([ 4, 13, 22, 31])

在本例中，我们索引到了(1, 0), (3, 1), (5, 2), (7, 3)四个元素。值得注意的是，采用与数组相同维度数量的整数数组或整数列表索引所得到的结果一定是一维数组。

以下我们来看一些复杂的索引案例，它通过索引行列来获得一个特定的矩形范围子集：

In [10]: arr[[1, 5, 7, 2]][:, [0, 3, 1, 2]]
Out[10]:
array([[ 4,  7,  5,  6],
       [20, 23, 21, 22],
       [28, 31, 29, 30],
       [ 8, 11,  9, 10]])

特别地，花式索引也是对原数组数据的复制，而不是切片索引或整数索引是返回原数据的视图：

In [11]: arr_copy = arr[[1, 3, 5, 7], [0, 1, 2, 3]]

In [12]: arr_copy
Out[12]: array([ 4, 13, 22, 31])

In [13]: arr
Out[13]:
array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11],
       [12, 13, 14, 15],
       [16, 17, 18, 19],
       [20, 21, 22, 23],
       [24, 25, 26, 27],
       [28, 29, 30, 31]])

In [14]: arr_copy[0] = 100

In [15]: arr_copy
Out[15]: array([100,  13,  22,  31])

In [16]: arr
Out[16]:
array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11],
       [12, 13, 14, 15],
       [16, 17, 18, 19],
       [20, 21, 22, 23],
       [24, 25, 26, 27],
       [28, 29, 30, 31]])

也可以通过花式索引直接对原数组赋值：

In [17]: arr[[1, 3, 5, 7], [0, 1, 2, 3]] = 0

In [18]: arr
Out[18]:
array([[ 0,  1,  2,  3],
       [ 0,  5,  6,  7],
       [ 8,  9, 10, 11],
       [12,  0, 14, 15],
       [16, 17, 18, 19],
       [20, 21,  0, 23],
       [24, 25, 26, 27],
       [28, 29, 30,  0]])

转置和轴交换

如果你学过线性代数，那你一定对转置很熟悉，在NumPy中也支持对数组进行转置，它会返回一个转置的数组，实际上也是原数组的视图。在NumPy中有transpose方法或数组的T属性来实现：

In [1]: import numpy as np

In [2]: arr = np.arange(15).reshape((3, 5))

In [3]: arr
Out[3]:
array([[ 0,  1,  2,  3,  4],
       [ 5,  6,  7,  8,  9],
       [10, 11, 12, 13, 14]])

In [4]: arr.T
Out[4]:
array([[ 0,  5, 10],
       [ 1,  6, 11],
       [ 2,  7, 12],
       [ 3,  8, 13],
       [ 4,  9, 14]])

对数组进行转置是一个很常见的运算，比如通过numpy.dot计算一个矩阵的内积时：

In [5]: arr = np.array([[0, 1, 0], [1, 2, -2], [6, 3, 2], [-1, 0, -1], [1, 0, 1]])

In [6]: arr
Out[6]:
array([[ 0,  1,  0],
       [ 1,  2, -2],
       [ 6,  3,  2],
       [-1,  0, -1],
       [ 1,  0,  1]])

In [7]: np.dot(arr.T, arr)
Out[7]:
array([[39, 20, 12],
       [20, 14,  2],
       [12,  2, 10]])

补充一点，通过@也可以实现矩阵乘法：

In [8]: arr.T @ arr
Out[8]:
array([[39, 20, 12],
       [20, 14,  2],
       [12,  2, 10]])

.T是一种简单交换轴的方法，ndarray类还提供了swapaxes方法，通过传入要交换的轴的索引来交换指定轴，其同样返回数据的视图而不是数据的副本：

In [9]: arr
Out[9]:
array([[ 0,  1,  0],
       [ 1,  2, -2],
       [ 6,  3,  2],
       [-1,  0, -1],
       [ 1,  0,  1]])

In [10]: arr.swapaxes(0,1)
Out[10]:
array([[ 0,  1,  6, -1,  1],
       [ 1,  2,  3,  0,  0],
       [ 0, -2,  2, -1,  1]])

NumPy随机数

NumPy的随机数模块numpy.random是在Python标准库random上的增强，优化在大量生成随机数的情况下的时间开销：

In [1]: import numpy as np

In [2]: np.random.standard_normal(size=(4, 4))
Out[2]:
array([[ 0.00206277,  0.60342769,  1.75782728, -0.25228312],
       [ 0.64817121,  0.6100538 ,  0.718226  ,  0.06148999],
       [ 1.83475916, -0.30223675,  0.14295896,  1.66922123],
       [ 0.23615696,  0.26534049, -0.93753573, -0.66522565]])

In [3]: from random import normalvariate

In [4]: N = 1_000_000

In [5]: %timeit samples = [normalvariate(0, 1) for _ in range(N)]
627 ms ± 9.02 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

In [6]: %timeit np.random.standard_normal(N)
29.1 ms ± 574 μs per loop (mean ± std. dev. of 7 runs, 10 loops each)

需要强调的是，这些随机并不是真正的随机，而是伪随机，其依赖于特定配置的生成器来生成确定性的数值。

生成器可以接受一个被称为“种子”的参数，这些种子决定了生成器的初始状态，而每次调用生成器都会影响其状态，伪随机性就通过这种不断的状态转移来产生伪随机数。

一般情况下，NumPy会调用其nunmpy.random中的默认生成器，必要情况下你可以自定义生成器。

In [7]: rng = np.random.default_rng(seed=12345)

In [8]: data = rng.standard_normal((2, 3))

In [9]: data
Out[9]:
array([[-1.42382504,  1.26372846, -0.87066174],
       [-0.25917323, -0.07534331, -0.74088465]])

In [10]: type(rng)
Out[10]: numpy.random._generator.Generator

方法	描述
permutation	打乱一个给定的序列，或打乱一个连续整数序列并返回
shuffle	随机打乱一个给定序列
uniform	从均匀分布中抽取样本
integers	从给定的低到高范围内随机抽取整数
standard_normal	从标准正态分布中抽取样本
binomial	从二项分布中抽取样本
normal	从正态（高斯）分布中抽取样本
beta	从β分布中抽取样本
chisquare	从卡方分布中抽取样本
gamma	从γ分布中抽取样本
uniform	从[0, 1)的均匀分布中抽取样本

通用函数——超高速的数组元素批量操作！

通用函数 (universal function)，或者说 ufunc，是能对ndarray对象中的数据进行元素级运算的函数，也可以将其视作快速向量化包装器——接受一个或多个标量并输出一个或多个标量结果的函数。

In [1]: import numpy as np

In [2]: arr = np.arange(10)

In [3]: arr
Out[3]: array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

In [4]: np.sqrt(arr)
Out[4]:
array([0.        , 1.        , 1.41421356, 1.73205081, 2.        ,
       2.23606798, 2.44948974, 2.64575131, 2.82842712, 3.        ])

In [5]: np.exp(arr)
Out[5]:
array([1.00000000e+00, 2.71828183e+00, 7.38905610e+00, 2.00855369e+01,
       5.45981500e+01, 1.48413159e+02, 4.03428793e+02, 1.09663316e+03,
       2.98095799e+03, 8.10308393e+03])

向量化 (Vectorization)

什么是向量化？

从最直观的角度上理解，向量化操作本身消除了我们在Python下显式使用for循环语句来处理整个数组，同时使我们的计算过程更加“数学”：

In [6]: a_arr = [1, 2, 3, 4]

In [7]: b_arr = [5, 6, 7, 8]

In [8]: c_arr = []

In [9]: for a, b in zip(a_arr, b_arr):
...:     c_arr.append(a+b)

In [10]: c_arr
Out[10]: [6, 8, 10, 12]

In [11]: a_arr = np.array([1, 2, 3, 4])

In [12]: b_arr = np.array([5, 6, 7, 8])

In [13]: c_arr = a_arr + b_arr

In [14]: c_arr
Out[14]: array([ 6,  8, 10, 12])

可以说，向量化本身赋予了我们批量操作数组中元素的能力，在编写代码的时候就可以避免很多不必要的工作（比如疯狂的写循环）。

当然，向量化本身也优化了大规模数据运算的时间开销，因为它将原本由Python解释器运行的循环转移到了底层C函数或Fortran函数，这些预编译的，经过高度优化的底层语言可以及其高效地循环处理数据运算，也使得SIMD（单指令多数据流）的优化成为可能。

对于一些特定的运算（比如线性代数里的），NumPy还会将其交给诸如BLAS或LAPACK这些久经考验的数值计算老战士，远比我们显式调用Python循环的效率来得高。

NumPy库中的所有通用函数都是向量化函数，实现了"win-to-win"——性能优异，语法友好。

numpy.sqrt或numpy.exp都被称为一元通用函数，因为它们只操作一个数组。而类似于numpy.add或者numpy.maximum等函数需要操作两个数组，这种被称为二元通用函数。

In [17]: x
Out[17]:
array([ 0.74762413,  0.93815547,  1.50833674,  0.07737313,  3.0463076 ,
       -0.37226118,  0.61122448,  0.50655983])

In [18]: y
Out[18]:
array([-0.84937302, -1.12331781, -2.61204501,  0.37888609, -1.77069753,
        0.51436005,  0.60106381,  0.08013947])

In [19]: np.maximum(x, y)
Out[19]:
array([0.74762413, 0.93815547, 1.50833674, 0.37888609, 3.0463076 ,
       0.51436005, 0.61122448, 0.50655983])

虽然不常见，但是有些通用函数一次可以返回多个值，比如numpy.modf：

In [20]: arr = np.random.standard_normal(5) * 10

In [21]: arr
Out[21]:
array([  3.89286933, -17.72821381,  -0.82537595,  12.79684213,
         0.05369509])

In [22]: remainder, whole_part = np.modf(arr)

In [23]: remainder
Out[23]: array([ 0.89286933, -0.72821381, -0.82537595,  0.79684213,  0.05369509])

In [24]: whole_part
Out[24]: array([  3., -17.,  -0.,  12.,   0.])

通用函数接受传入一个out参数，这样他们会将结果写入一个已经存在的数组，而不是新建一个数组：

In [26]: out
Out[26]: array([0., 0., 0., 0., 0.])

In [27]: np.add(arr, 1)
Out[27]:
array([  4.89286933, -16.72821381,   0.17462405,  13.79684213,
         1.05369509])

In [28]: np.add(arr, 1, out=out)
Out[28]:
array([  4.89286933, -16.72821381,   0.17462405,  13.79684213,
         1.05369509])

In [29]: out
Out[29]:
array([  4.89286933, -16.72821381,   0.17462405,  13.79684213,
         1.05369509])

以下表格列举了一些NumPy提供的一元通用函数：

Function	Description
abs, fabs	逐元素计算整数、浮点数或复数的绝对值
sqrt	计算每个元素的平方根（等价于 arr ** 0.5）
square	计算每个元素的平方（等价于 arr ** 2）
exp	计算每个元素的指数 e^x
log, log10, log2, log1p	自然对数（以 e 为底）、以 10 为底的对数、以 2 为底的对数，以及 log(1 + x)，分别对应
sign	计算每个元素的符号：1（正数）、0（零）或 -1（负数）
ceil	计算每个元素的向上取整（即大于等于该数的最小整数）
floor	计算每个元素的向下取整（即小于等于该数的最大整数）
rint	将元素四舍五入到最接近的整数，保持数据类型不变
modf	返回数组的小数部分和整数部分作为两个独立的数组
isnan	返回布尔数组，指示每个值是否为 NaN（非数字）
isfinite, isinf	返回布尔数组，分别指示每个元素是否为有限值（非无穷、非 NaN）或无穷大
cos, cosh, sin, sinh, tan, tanh	常规三角函数和双曲三角函数
arccos, arccosh, arcsin, arcsinh, arctan, arctanh	反三角函数和反双曲函数
logical_not	逐元素计算逻辑非（等价N于 ~arr）

以下表格列举了一些NumPy二元通用函数：

Function	Description
add	对数组中对应元素进行相加
subtract	从第一个数组的元素中减去第二个数组的元素
multiply	对数组元素进行乘法运算
divide, floor_divide	除法或向下取整除法（舍弃余数）
power	将第一个数组的元素提升到第二个数组所指示的幂次
maximum, fmax	逐元素计算最大值；fmax 忽略 NaN 值
minimum, fmin	逐元素计算最小值；fmin 忽略 NaN 值
mod	逐元素计算模运算（除法的余数）
copysign	将第二个参数的符号复制到第一个参数的数值上
greater, greater_equal, less, less_equal, equal, not_equal	执行逐元素比较，返回布尔数组（等价于中缀操作符 >, >=, <, <=, ==, !=）
logical_and	逐元素计算逻辑与 (&) 操作的真值
logical_or	逐元素计算逻辑或 (\|) 操作的真值
logical_xor	逐元素计算逻辑异或 (^) 操作的真值

面向数组编程

NumPy库的出现代表着面向数组编程这一思想从MATLAB等科学语言到Python的迁移，参照Python“万物皆对象”，NumPy可以说是“万物皆数组”，它的好处我们之前提到了不少，这里再次总结一下：

使用简洁的数组表达式代替显式循环，代码可读性更好
数组在计算过程中以向量化的方式驱动，效率更高
NumPy提供的广播机制使得Python下的面向数组编程更加“丝滑”

接下来让我们以简单的实例来看看面向数组编程的风格：

假设我们想要在一个直角坐标系中的网格点上计算各个格点坐标的\(\sqrt{x^2 + y^2}\)，首先我们需要建立所有网格点坐标的数组，其次将其用于计算原点矩。

In [1]: import numpy as np

In [2]: points = np.arange(-5, 5, 0.01)

In [3]: xs, ys = np.meshgrid(points, points)

In [4]: ys
Out[4]:
array([[-5.  , -5.  , -5.  , ..., -5.  , -5.  , -5.  ],
       [-4.99, -4.99, -4.99, ..., -4.99, -4.99, -4.99],
       [-4.98, -4.98, -4.98, ..., -4.98, -4.98, -4.98],
       ...,
       [ 4.97,  4.97,  4.97, ...,  4.97,  4.97,  4.97],
       [ 4.98,  4.98,  4.98, ...,  4.98,  4.98,  4.98],
       [ 4.99,  4.99,  4.99, ...,  4.99,  4.99,  4.99]],
      shape=(1000, 1000))

numpy.meshgrid函数在这里的作用就是：根据你给的坐标轴范围，生成对应各个轴的坐标点，所以Y轴上是列重复，X轴是行重复数组（可以想想平面坐标系上，一个矩形框住了一个区域）。

然后我们需要根据格点坐标来计算各个点上的原点矩：

In [5]: z = np.sqrt(xs**2 + ys**2)

In [6]: z
Out[6]:
array([[7.07106781, 7.06400028, 7.05693985, ..., 7.04988652, 7.05693985,
        7.06400028],
       [7.06400028, 7.05692568, 7.04985815, ..., 7.04279774, 7.04985815,
        7.05692568],
       [7.05693985, 7.04985815, 7.04278354, ..., 7.03571603, 7.04278354,
        7.04985815],
       ...,
       [7.04988652, 7.04279774, 7.03571603, ..., 7.0286414 , 7.03571603,
        7.04279774],
       [7.05693985, 7.04985815, 7.04278354, ..., 7.03571603, 7.04278354,
        7.04985815],
       [7.06400028, 7.05692568, 7.04985815, ..., 7.04279774, 7.04985815,
        7.05692568]], shape=(1000, 1000))

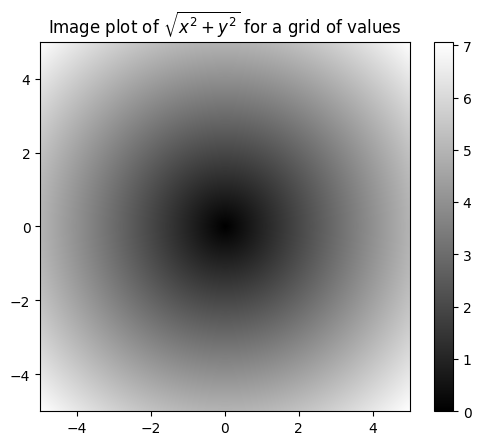
最后，算是一个提前预告，我们可以用matplolib把它画出来：

In [7]: import matplotlib.pyplot as plt

In [8]: plt.imshow(z, cmap=plt.cm.gray, extent=[-5, 5, -5, 5])
Out[8]: <matplotlib.image.AxesImage at 0x7767bad79ac0>

In [9]: plt.colorbar()
Out[9]: <matplotlib.colorbar.Colorbar at 0x7767bada6b10>

In [10]: plt.title("Image plot of $\sqrt{x^2 + y^2}$ for a grid of values")
<>:1: SyntaxWarning: invalid escape sequence '\s'
<ipython-input-10-9f3ef7d92a19>:1: SyntaxWarning: invalid escape sequence '\s'
  plt.title("Image plot of $\sqrt{x^2 + y^2}$ for a grid of values")
Out[10]: Text(0.5, 1.0, 'Image plot of $\\sqrt{x^2 + y^2}$ for a grid of values')

alt text

向量化消歧义

在计算机科学的其他领域内有对“向量化”的不同指代or解释，但是本笔记特指NumPy对整个数组批量操作的过程。

逻辑表达式与数组运算

简单的数学运算显然不能满足我们的胃口，如何将那些在Python中经常写的逻辑表达式（比如三目运算/三元运算，称呼随你喜欢）转化为向量化的数组运算？NumPy早就考虑好了！

假如我们有xarr与yarr两个数组，有一个布尔数组cond，想实现“当cond为真时候，取xarr值，否则取yarr的值”，如果用Python List的视角来看，它就要这么处理：

import numpy as np

xarr = np.array([1.1, 1.2, 1.3, 1.4, 1.5])
yarr = np.array([2.1, 2.2, 2.3, 2.4, 2.5])
cond = np.array([True, False, True, True, False])

results = [(x if c else y) for x, y, c in zip(xarr, yarr, cond)]

首先，面对大数组时候，循环太慢了！其次，如果是多维的嵌套数组就更加棘手了！

假如我们使用numpy.where函数，这个NumPy提供的向量化版本的三元表达式，那就很简单了：

In [2]: xarr = np.array([1.1, 1.2, 1.3, 1.4, 1.5])

In [3]: yarr = np.array([2.1, 2.2, 2.3, 2.4, 2.5])

In [4]: cond = np.array([True, False, True, True, False])

In [5]: results = np.where(cond, xarr, yarr)

In [6]: results
Out[6]: array([1.1, 2.2, 1.3, 1.4, 2.5])

numpy.where函数的第二，三个参数不必是数组形式，可以是标量。其一个经典场景是生成一个新数组，比如有一个随机生成的数组，你想将负数置换为'-2'，正数置换为'2'：

In [7]: arr = np.random.standard_normal((4, 4))

In [8]: arr
Out[8]:
array([[ 0.33711373, -1.62057533,  0.33826943,  0.20302062],
       [ 1.108013  , -0.50193579,  0.32476979, -0.64504127],
       [ 1.07732731,  1.18537251,  1.31761483,  1.03421576],
       [-1.23994351,  1.13117754,  0.01499102, -1.43553695]])

In [9]: np.where(arr > 0, 2, -2)
Out[9]:
array([[ 2, -2,  2,  2],
       [ 2, -2,  2, -2],
       [ 2,  2,  2,  2],
       [-2,  2,  2, -2]])

你也可以将标量和数组混合使用，以实现部分替换的效果：

In [10]: np.where(arr > 0, 2, arr)
Out[10]:
array([[ 2.        , -1.62057533,  2.        ,  2.        ],
       [ 2.        , -0.50193579,  2.        , -0.64504127],
       [ 2.        ,  2.        ,  2.        ,  2.        ],
       [-1.23994351,  2.        ,  2.        , -1.43553695]])

NumPy与数理统计

NumPy提供了众多数理统计函数，实现了对数组的求和、均值与标准差计算，这些函数被称为聚合函数（有时候被称为归约操作）。这些函数既可以以实例方法的方式调用，也可以通过NumPy的顶层函数调用，当使用后者时候，需要将待数组作为第一个参数传入。

In [1]: import numpy as np

In [2]: arr = np.random.standard_normal((5, 4))

In [3]: arr
Out[3]:
array([[ 0.71755259,  0.20358816,  1.36127288, -1.05343062],
       [ 0.76511967, -0.18051514,  1.02303924,  0.42781514],
       [ 1.02475739,  1.09368618, -0.40281465, -0.4973147 ],
       [-1.48682195, -0.25148641, -0.22010944, -0.10937172],
       [ 0.30455732,  1.86131733, -1.26783951, -0.93971192]])

In [4]: arr.mean()
Out[4]: np.float64(0.11866449224624816)

In [5]: np.mean(arr)
Out[5]: np.float64(0.11866449224624816)

In [6]: arr.sum()
Out[6]: np.float64(2.373289844924963)

诸如求均值或求和等函数都可以接受一个轴参数，以指定在哪个轴上做计算，最终得到一个维度减一的数组：

In [7]: arr.mean(axis=1)
Out[7]: array([ 0.30724576,  0.50886473,  0.30457856, -0.51694738, -0.0104192 ])

In [8]: arr.sum(axis=0)
Out[8]: array([ 1.32516502,  2.72659013,  0.49354852, -2.17201382])

其中arr.mean(axis=1)表示沿列求平均，arr.sum(axis=0)表示沿行求和。

其他类似于numpy.cumsum等函数则不进行聚合，相反，他们会返回存储中间结果的数组，这被称为累积函数：

In [9]: arr = np.arange(9)

In [10]: arr
Out[10]: array([0, 1, 2, 3, 4, 5, 6, 7, 8])

In [11]: arr.cumsum()
Out[11]: array([ 0,  1,  3,  6, 10, 15, 21, 28, 36])

对于多维数组，累积函数会返回一个相同大小的数组，如果指定axis参数，则可以指定累计函数的累积方向：

In [12]: arr = np.array([[0, 1, 2], [3, 4, 5], [6, 7, 8]])

In [13]: arr
Out[13]:
array([[0, 1, 2],
       [3, 4, 5],
       [6, 7, 8]])

In [14]: arr.cumsum(axis=0)
Out[14]:
array([[ 0,  1,  2],
       [ 3,  5,  7],
       [ 9, 12, 15]])

In [15]: arr.cumsum(axis=1)
Out[15]:
array([[ 0,  1,  3],
       [ 3,  7, 12],
       [ 6, 13, 21]])

下表展示了部分常见的数理统计函数：

Method	Description
sum	计算数组中所有元素的总和，或沿某个轴进行求和；零长度数组的和为 0
mean	算术平均值；在零长度数组上无效（返回 NaN）
std, var	标准差和方差，分别对应
min, max	最小值和最大值
argmin, argmax	最小值和最大值元素的索引，分别对应
cumsum	从 0 开始的元素累积和
cumprod	从 1 开始的元素累积积

布尔数组

布尔数组在上述方法中，True会被视作1，而False会被视作0。因此一种常见的用法是利用sum函数布尔数组中真值的数量：

In [1]: import numpy as np

In [2]: arr = np.random.standard_normal(100)

In [3]: (arr > 0).sum()
Out[3]: np.int64(48)

In [4]: (arr <= 0).sum()
Out[4]: np.int64(52)

有两个方法也很好用，any会检查数组中是否有一个或多个值为真，而all会检查数组中是否所有值都为真。

In [5]: bools = np.array([False, False, True, False])

In [6]: bools.any()
Out[6]: np.True_

In [7]: bools.all()
Out[7]: np.False_

这个方法也适合非布尔数组，所有非零元素会被视作真。

排序

与Python内置列表类似，NumPy数组也提供了sort方法对数组进行原地排序。

In [1]: import numpy as np

In [2]: arr = np.random.standard_normal(6)

In [3]: arr
Out[3]:
array([ 0.60233051, -0.05898702,  0.458996  ,  1.73333703, -0.30045633,
        0.62526467])

In [4]: arr.sort()

In [5]: arr
Out[5]:
array([-0.30045633, -0.05898702,  0.458996  ,  0.60233051,  0.62526467,  1.73333703])

通过传递axis参数，可以指定sort对某一个轴进行原地排序。

In [6]: arr = np.random.standard_normal((5, 3))

In [7]: arr
Out[7]:
array([[-0.27631334, -0.66668102, -0.01554847],
       [ 1.0062891 ,  1.82714433, -0.47142011],
       [-1.70240089,  0.69923053,  1.61688779],
       [-0.71986253, -0.26518041, -0.7797188 ],
       [-0.11775361, -0.55898711, -0.28750949]])

In [8]: arr.sort(axis=0)

In [9]: arr
Out[9]:
array([[-1.70240089, -0.66668102, -0.7797188 ],
       [-0.71986253, -0.55898711, -0.47142011],
       [-0.27631334, -0.26518041, -0.28750949],
       [-0.11775361,  0.69923053, -0.01554847],
       [ 1.0062891 ,  1.82714433,  1.61688779]])

In [10]: arr.sort(axis=1)

In [11]: arr
Out[11]:
array([[-1.70240089, -0.7797188 , -0.66668102],
       [-0.71986253, -0.55898711, -0.47142011],
       [-0.28750949, -0.27631334, -0.26518041],
       [-0.11775361, -0.01554847,  0.69923053],
       [ 1.0062891 ,  1.61688779,  1.82714433]])

其中，arr.sort(axis=0)是沿行（也就是对每个列）进行排序，arr.sort(axis=1)是沿列（也就是对每行）进行排序。

轴参数

一开始对NumPy的axis参数有比较大的误解，特别是二维数组中，axis=0是以列为单位做修改而不是行与我的直觉相悖。

不过这实际上要这么理解，在多维数组中我们对变量的引用可以通过递归使用下标法来引用，比如arr[0][0]，其中第一个下标的位置就是axis=0，第二个则是axis=1。

而我们指定轴编号实际上就是指定了沿着哪个轴方向，假如我们指定了axis=0，那么我们可以想象每次操作，NumPy都会固定一个列（比如第一列），然后遍历同列不同行的元素（沿着行方向）做操作。

使用numpy.sort函数会返回数组的排序副本而不会原地修改数组（类似于Python中的sorted函数）。

In [12]: arr2 = np.array([5, -10, 7, 1, 0, -3])

In [13]: sorted_arr2 = np.sort(arr2)

In [14]: sorted_arr2
Out[14]: array([-10,  -3,   0,   1,   5,   7])

集合

NumPy的数组提供了一些基本的集合操作，比如numpy.unique，它会返回数组中排序后的唯一值（排序+去重）：

In [1]: import numpy as np

In [2]: names = np.array(["Bob", "Will", "Joe", "Bob", "Will", "Joe", "Joe"])

In [3]: np.unique(names)
Out[3]: array(['Bob', 'Joe', 'Will'], dtype='<U4')

In [4]: ints = np.array([3, 3, 3, 2, 2, 1, 1, 4, 4])

In [5]: np.unique(ints)
Out[5]: array([1, 2, 3, 4])

对比Python原生的方法：

In [6]: sorted(set(names))
Out[6]: [np.str_('Bob'), np.str_('Joe'), np.str_('Will')]

在大多数情况下，NumPy的numpy.unique方法都比Python的原生方法要更快，返回类型为ndarray。

此外，NumPy还提供了一个numpy.isin函数，它用来判断一个数组中的值是否在另一个数组内，返回布尔数组：

In [7]: values = np.array([6, 0, 0, 3, 2, 5, 6])

In [8]: np.isin(values, [2, 3, 6])
Out[8]: array([ True, False, False,  True,  True, False,  True])

下表展示了NumPy中一些常用的集合操作：

Method	Description
unique(x)	计算 x 中排序后的唯一元素
intersect1d(x, y)	计算 x 和 y 中共有的、排序后的元素
union1d(x, y)	计算 x 和 y 的排序并集
in1d(x, y)	计算一个布尔数组，指示 x 中每个元素是否在 y 中存在
setdiff1d(x, y)	集合差集：x 中不在 y 中的元素
setxor1d(x, y)	集合对称差集：存在于任一数组中但不同时存在于两个数组中的元素

数组与件操作

出乎意料吧，NumPy的数组支持直接导出为文件或从文件中加载，其支持以文本或二进制格式在磁盘上进行数据的存取。

因为大多数人更倾向于使用pandas等工具来处理表格数据，我们重点介绍NumPy的内置二进制格式。

numpy.save和numpy.load是实现数组数据存取的两大核心函数，默认情况下数组数据以未压缩的原始二进制格式报错，文件扩展名为.npy：

In [1]: import numpy as np

In [2]: arr = np.arange(10)

In [3]: np.save("some_array", arr)

In [4]: np.load("some_array.npy")
Out[4]: array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

Tip

如果调用numpy.save时传入的文件名不是以.npy结尾的，NumPy会自动将其补齐。

你可以使用numpy.savez来一次性打包多个数组并只输出一个未经压缩的文件：

In [5]: np.savez("array_archive.npz", a=arr, b=arr)

In [6]: arch = np.load("array_archive.npz")

In [7]: arch['b']
Out[7]: array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

如果可以的话，非常建议使用numpy.savez_compressed函数，它可以将数据压缩保存：

In [8]: np.savez_compressed("arrays_compressed.npz", a=arr, b=arr)

线性代数

线性代数的运算（如矩阵乘法、分解、行列式等方阵运算）是数组运算的一大核心功能，但在NumPy中，诸如数组A * 数组B的乘法运算是元素级的运算，要真正实现矩阵乘法，NumPy为其专门提供了numpy.dot函数，也有与之类似的类方法.dot：

In [1]: import numpy as np

In [2]: x = np.array([[1., 2., 3.], [4., 5., 6.]])

In [3]: y = np.array([[6., 23.], [-1, 7], [8, 9]])

In [4]: x
Out[4]:
array([[1., 2., 3.],
       [4., 5., 6.]])

In [5]: y
Out[5]:
array([[ 6., 23.],
       [-1.,  7.],
       [ 8.,  9.]])

In [6]: x.dot(y)
Out[6]:
array([[ 28.,  64.],
       [ 67., 181.]])

In [7]: np.dot(x, y)
Out[7]:
array([[ 28.,  64.],
       [ 67., 181.]])

@运算法也代表矩阵乘法：

In [8]: x @ np.ones(3)
Out[8]: array([ 6., 15.])

numpy.linalg是NumPy自带的线性代数模块，提供了一系列标准的矩阵分解方法，比如求逆inv，或QR分解qr：

In [9]: from numpy.linalg import inv

In [10]: from numpy import random

In [11]: X = random.standard_normal((4, 4))

In [12]: mat = X.T @ X

In [13]: inv(mat)
Out[13]:
array([[ 577.51382089,  335.65802252,  701.02002887, -819.15603686],
       [ 335.65802252,  196.54686044,  409.85998119, -477.25436255],
       [ 701.02002887,  409.85998119,  856.30339218, -997.89532881],
       [-819.15603686, -477.25436255, -997.89532881, 1166.35607481]])

In [14]: mat @ inv(mat)
Out[14]:
array([[ 1.00000000e+00, -2.93696062e-14, -2.82889210e-13,
         2.44522839e-14],
       [-2.42855859e-14,  1.00000000e+00,  4.31185966e-14,
         8.37913161e-16],
       [ 1.44866179e-13,  1.50640144e-14,  1.00000000e+00,
        -1.77608083e-13],
       [ 2.44116991e-14, -3.26129943e-14, -1.60805823e-13,
         1.00000000e+00]])

In [15]: np.set_printoptions(suppress=True, precision=5)

In [16]: mat @ inv(mat)
Out[16]:
array([[ 1., -0., -0.,  0.],
       [-0.,  1.,  0.,  0.],
       [ 0.,  0.,  1., -0.],
       [ 0., -0., -0.,  1.]])

浮点数精度

计算机不能精确表示绝大多数实数，因为浮点数的精度是有限的（即使是64位的浮点数，它的位数也是有限的，所以其也只能表示2^64种可能），所以最后的计算结果会有极其微小的误差（就像上面展示的那样）。

这里我使用了np.set_printoptions(suppress=True, precision=5)来格式化numpy的打印结果。

数组编程与随机游走

我们通过一个实际案例来感受一下NumPy所秉持的面向数组思想：

随机游走是一种基于随机数的游走过程，最简单的形式是从0开始，每次随机决定+1或者-1，以下内容在VSCode Jupyter内运行：

import numpy as np
from numpy import random

nsteps = 1000
draws  = random.randint(0, 2, size=nsteps)

steps  = np.where(draws == 0, -1, 1)
walk   = steps.cumsum()

walk.min()
# np.int64(-22)

walk.max()
# np.int64(29)

# 更复杂的指标是首次穿越，比如第一次里原点10格远是哪一步？
# argmax()会返回数组中最大值首次出现的索引
(np.abs(walk) >= 10).argmax()
# np.int64(137)

有时候我们想要一次模拟大量的游走情况，比如5000次，NumPy的高效将得到充分体现：

nwalks = 5000
nsteps = 1000

draws  = random.randint(0, 2, size=(nwalks, nsteps))
steps  = np.where(draws == 0, -1, 1)

walks  = steps.cumsum(axis=1)
walks
# array([[  1,   2,   3, ...,   0,   1,   2],
#        [ -1,  -2,  -1, ..., -42, -43, -42],
#        [  1,   2,   1, ...,  14,  15,  14],
#        ...,
#        [ -1,  -2,  -1, ...,   0,  -1,  -2],
#        [ -1,   0,  -1, ..., -36, -35, -34],
#        [  1,   0,  -1, ...,  50,  49,  48]], shape=(5000, 1000))

walks.max()
# np.int64(120)

walks.min()
# np.int64(-125)

# 筛选出距原点距离达到30格的walks
hits30 = (np.abs(walks) >= 30).any(axis=1)
hits30
# array([False,  True, False, ...,  True,  True,  True], shape=(5000,))

hits30.sum()
# np.int64(3310)

crossing_times = (np.abs(walks[hits30]) >= 30).argmax(axis=1)
crossing_times
# array([341, 253, 123, ..., 483, 229, 475], shape=(3310,))

crossing_times.mean()
# np.float64(504.2235649546828)